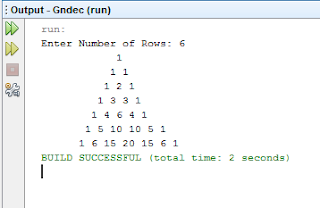
Following Code Will print the Rhombus Structure :
Code::
import java.util.*;
public class Rhombus
{
public static void main(String[] nt)
{
Scanner in=new Scanner(System.in);
System.out.print("Enter Number of Rows: ");
int n=in.nextInt();
int count=1,c,space=0;
for(int i=1;i<2*n;i++)
{
if(i<=n)
{
c=i;
space++;
}
else
{
c=2*n-i;
space--;
}
for(int spc=n-space;spc>0;spc--)
{
System.out.print(" ");
}
for(int j=0;j<count;j++)
{
System.out.print(c);
if(j<count/2)
{
c--;
}
else
{
c++;
}
}
if(i<n)
{
count=count+2;
}
else
{
count=count-2;
}
System.out.println();
}
}
}
Output::
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients.
Pascal Triangle:
Code::
import java.util.*;
public class PascalTriangle
{
public static void main(String[] nt)
{
Scanner in=new Scanner(System.in);
System.out.print("Enter Number of Rows: ");
int n=in.nextInt();
int [][] a=new int[n+1][];
for(int i=0;i<=n;i++)
{
a[i]=new int[i+1]; //jagged array
}
for(int i=0;i<=n;i++)
{ a[i][0]=1;
a[i][i]=1;
}
for(int i=2;i<=n;i++)
{
for(int j=1;j<i;j++)
{
a[i][j]=a[i-1][j-1]+a[i-1][j];
}
}
for(int i=0;i<=n;i++)
{
for(int spc=2*n-i;spc>0;spc--)
{
System.out.print(" ");
}
for(int j=0;j<=i;j++)
{
System.out.print(a[i][j]+" ");
}
System.out.println();
}
}
}
Output::
Question::
Consider the sequence of digits from 1 through N (N<=9) in increasing order: 1 2 3 4 … N Insert either a ‘+’ (for addition) or a ‘-‘ (for subtraction) between each of the digits so that the resultant sum is zero. Print all possible combinations that sum to zero.
Example: Enter a number: 7
1+2-3+4-5-6+7=0
1+2-3-4+5+6-7=0
1-2+3+4-5+6-7=0
1-2-3-4-5+6+7=0
Code::
import java.util.*;
class sequencer
{
int n; //for no of terms
int b=1,c=1,d=1,e=1,f=1,g=1,h=1; //for different combinations
int[] a=new int[10]; //for saving all values
Scanner in=new Scanner(System.in);
public void combinations() {
System.out.print("Enter Number of Terms (N<=9):");
n=in.nextInt();
for(int i=0;i<n;i++)
{
a[i]=i+1; //assigning values
}
double s=Math.pow(2,n-1); //total combinations
int k=1;
System.out.println("Combinations are:");
while(k<=s)
{ int sum=a[0];
for(int i=1;i<n;i++)
{
sum=sum+a[i]; //checking sum
}
if(sum==0)
{
for(int i=0;i<n;i++)
System.out.print(a[i]+" ");
System.out.println(" =0");
}
change(a);
k++;
}
}
public void change(int[] a)
{
a[n-1]=-a[n-1];
if(n==2) return;
if(b==2)
{
a[n-2]=-a[n-2];
b=1;
}
else
{
b++;
}
if(n==3) return;
if(c==4)
{
a[n-3]=-a[n-3];
c=1;
}
else
{
c++;
}
if(n==4) return;
if(d==8)
{
a[n-4]=-a[n-4];
d=1;
}
else
{
d++;
}
if(n==5) return;
if(e==16)
{
a[n-5]=-a[n-5];
e=1;
}
else
{
e++;
}
if(n==6) return;
if(f==32)
{
a[n-6]=-a[n-6];
f=1;
}
else
{
f++;
}
if(n==7) return;
if(g==64)
{
a[n-7]=-a[n-7];
g=1;
}
else
{
g++;
}
if(n==8) return;
if(h==128)
{
a[n-8]=-a[n-8];
h=1;
}
else
{
h++;
}
if(n==9) return;
}
}
public class AllIsNothing {
public static void main(String [] nt)
{
sequencer ob=new sequencer();
ob.combinations();
}
}
Output::
Special Thanks To Miss Hargun and Miss Aaishwarya for this program
Following Code Calculate The Square Root of a Number Without using sqrt function:
Code::
import java.util.*;
public class Squareroot
{
public static void main(String[] nt)
{ Scanner in=new Scanner(System.in);
double beg=0,end,n;
System.out.print("Enter Number:");
n=in.nextDouble();
end=n;
double prevmid=0,mid=(beg+end)/2;
double dif=Math.abs(mid-prevmid);
while(mid*mid!=n&&dif>0.000005)
{
if(mid*mid>n)
{
end=mid;
}
else
{
beg=mid;
}
prevmid=mid;
mid=(beg+end)/2;
dif=Math.abs(mid-prevmid);
}
System.out.println("Square Root is: "+mid);
}
}
Output::
Following Code will print a Diamond Pattern of User Specified Number of Rows:
Code::
import java.util.*;
public class Pattern
{
public static void main(String[] nt)
{
Scanner in=new Scanner(System.in);
System.out.print("Enter number of Rows: ");
int n=in.nextInt();
for(int i=1;i<=n;i++)
{
for(int sp=n-i;sp>0;sp--)
{
System.out.print(" ");
}
for(int j=0;j<i;j++)
{
System.out.print("* ");
}
System.out.println();
}
for(int i=n;i>0;i--)
{
for(int sp=0;sp<n-i;sp++)
{
System.out.print(" ");
}
for(int j=0;j<i;j++)
{
System.out.print("* ");
}
System.out.println();
}
}
}
Output::
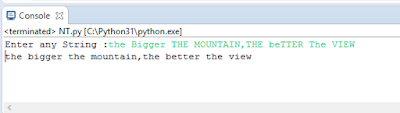
Following code will define a lower function to convert all letters of a string to lower case:
Code::
def lower(a):
x=""
for i in a:
if(i>='A' and i<'a'):
x=x+((chr((ord(i)+32)))) #ord to convert character to ascii value
else:
x=x+i
return x
i=input("Enter any String :")
print(lower(i))
Output::
Following code defines a function upper which changes the entered string to Upper Case:
Code::
def upper(a):
x="" #for returning Upper Case
for i in a:
if(i>='a'): #for Not Changing Already upper Case Letters
x=x+((chr((ord(i)-32))))
else:
x=x+i
return x
i=input("Enter any String :")
print(upper(i))
Output::