Kruskal's Algoritm DAA

Question: Write a program to find the minimum cost of connecting all the engineering colleges in your state using Kruskal's algorithm.
Code:

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;

public class Kruskal {

    static  class  edge{
        int distance,s,d;

        public edge(int distance, int s, int d) {
            this.distance = distance;
            this.s = s;
            this.d = d;
        }

        @Override        public String toString() {
            return "edge{" +
                    "distance=" + distance +
                    ", s=" + s +
                    ", d=" + d +
                    '}';
        }
    }

    public static void main(String[] nt){

        int graph[][]= {{0, 2, 0, 6, 0},
                {2, 0, 3, 8, 5},
                {0, 3, 0, 0, 7},
                {6, 8, 0, 0, 9},
                {0, 5, 7, 9, 0},
        };

        boolean[] visited=new boolean[graph.length];
        ArrayList<edge>edgeArrayList=new ArrayList<>();

        for(int i=0;i<graph.length;i++){
            visited[i]=false;
            for(int x=0;x<graph[i].length;x++){
                if(graph[i][x]!=0){
                    edgeArrayList.add(new edge(graph[i][x],i,x));
                }
            }
        }

        Collections.sort(edgeArrayList, new Comparator<edge>() {
            @Override            public int compare(edge edge, edge t1) {
                return edge.distance-t1.distance;
            }
        });
        int count=0;
        edge edgenow;
        int min=0;
        while (count!=graph.length-1){
            edgenow=edgeArrayList.get(0);
            edgeArrayList.remove(0);
            if(visited[edgenow.d]==false || visited[edgenow.s]==false){
                min+=edgenow.distance;
               System.out.println((edgenow.s+1)+" -> "+(edgenow.d+1)+" : "+edgenow.distance);
                visited[edgenow.d]=true;
                visited[edgenow.s]=true;
                count++;
            }
        }
        System.out.println("Cost is : "+min);
    }
}

Output:

Dijkstra’s algorithm.

Question: Write a program to find shortest path from your home to college using Dijkstra’s algorithm.

Code:

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;

public class Dijkstras {

    static class vertex{
        int distance;
        boolean visited;
        int no;
        int previous;

        @Override        public String toString() {
            return "vertex{" +
                    "distance=" + distance +
                    ", visited=" + visited +
                    ", no=" + (no+1) +
                    ", previous=" + (previous+1) +
                    '}';
        }

        public vertex(int distance, boolean visited, int no, int previous) {
            this.distance = distance;
            this.visited = visited;
            this.no = no;
            this.previous = previous;
        }


    }

    public static void main(String[] nt){
        ArrayList<vertex> arrayList=new ArrayList<>();
        ArrayList<vertex> result=new ArrayList<>();
       /* int graph[][] = new int[][]{{0, 4, 0, 0, 0, 0, 0, 8, 0},                {4, 0, 8, 0, 0, 0, 0, 11, 0},                {0, 8, 0, 7, 0, 4, 0, 0, 2},                {0, 0, 7, 0, 9, 14, 0, 0, 0},                {0, 0, 0, 9, 0, 10, 0, 0, 0},                {0, 0, 4, 14, 10, 0, 2, 0, 0},                {0, 0, 0, 0, 0, 2, 0, 1, 6},                {8, 11, 0, 0, 0, 0, 1, 0, 7},                {0, 0, 2, 0, 0, 0, 6, 7, 0}        };       */       int[][] graph={{0,4,8,0,0},{0,0,5,8,10},{0,4,0,0,3},{0,0,0,0,6},{0,0,0,7,0}};
       for (int i=0;i<graph.length;i++){
            arrayList.add(new vertex(Integer.MAX_VALUE,false,i,Integer.MAX_VALUE));
        }

        arrayList.get(0).distance=0;
        arrayList.get(0).previous=0;

        Comparator<vertex> com=new Comparator<vertex>() {
            @Override            public int compare(vertex vertex, vertex t1) {
                return vertex.distance-t1.distance;
            }
        };

        vertex poped;
        while (arrayList.size()!=0){
            Collections.sort(arrayList,com);
            poped=arrayList.get(0);
            arrayList.remove(0);


            if(poped.visited==false){
                for (int i=0;i<graph[poped.no].length;i++){
                    if(graph[poped.no][i]!=0&& find(arrayList,i)!=Integer.MAX_VALUE){
                        int x=find(arrayList,i);
                            if(graph[poped.no][i]+poped.distance<arrayList.get(x).distance){
                                arrayList.get(x).distance=graph[poped.no][i]+poped.distance;
                                arrayList.get(x).previous=poped.no;
                            }
                    }
                }
                poped.visited=true;
                result.add(poped);
            }
        }

        Comparator<vertex>comp2=new Comparator<vertex>() {
            @Override            public int compare(vertex vertex, vertex t1) {
                return vertex.no-t1.no;
            }
        };
        Collections.sort(result,comp2);
        for(int i=0;i<result.size();i++){

            System.out.println(result.get(i).toString());
        }

    }

    static int find(ArrayList<vertex> arrayList,int n){
        int i=Integer.MAX_VALUE;

        for (int x=0;x<arrayList.size();x++){
            if(arrayList.get(x).no==n){
                return x;
            }
        }
        return i;
    }
}

Output:

Travelling Salesman Problem

Question:

Code:
Write a program to find minimum route for a newspaper distributer of your locality using Greedy algorithm. 

public class Dmain {

    public static void main(String[] nt){

        int n=5;
        int[][] c={{0,3,Integer.MAX_VALUE,7,Integer.MAX_VALUE,3},{3,0,2,Integer.MAX_VALUE,6,Integer.MAX_VALUE},{Integer.MAX_VALUE,2,0,2,5,Integer.MAX_VALUE},
                {7,Integer.MAX_VALUE,2,0,1,Integer.MAX_VALUE},
                {Integer.MAX_VALUE,6,5,1,0,4},
                {3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,4,0}
                    };

        /*int[][] d={                {1,2,3,4},                {5,6,7,8},                {3,4,5,6},                {9,8,4,3}        };*/
        System.out.println("Shorest Path is : "+find(c));
    }

    static StringBuffer find(int[][] c){
        StringBuffer buffer=new StringBuffer();
        boolean [] present=new boolean[c.length];
        for(int i=0;i<c.length;i++){
            present[i]=false;
        }
        int count=1,node=0,cost=0,previous=0;
        present[node]=true;
        while(count!=c.length+1){
            int min=Integer.MAX_VALUE,minindex=0;
            for(int i=0;i<c[node].length;i++){
                if(present[i]==false && min>c[node][i]){
                        min=c[node][i];
                        minindex=i;
                }
            }
            present[minindex]=true;
            if(min!=Integer.MAX_VALUE){ cost+=min;}
            buffer.append((node+1)+"->");
            previous=node;
            node=minindex;
            count++;
        }
        buffer.append("1"+"\nMinimum Cost Is : "+(cost+c[previous][0]));
        return buffer;
    }

}

Output:

Prim's Java DAA 6

Code:

import java.util.ArrayList;

public class Prims {

   static class Vertex{
        int parent;
        boolean set;
        int key;


        public Vertex(int parent, boolean set, int key) {
            this.parent = parent;
            this.set = set;
            this.key = key;
        }

       @Override       public String toString() {
           return "Vertex{" +
                   "parent=" + parent +
                   ", set=" + set +
                   ", key=" + key +
                   '}';
       }
   }

    public static void main(String[] nt){

        int graph[][]= {{0, 2, 0, 6, 0},
                {2, 0, 3, 8, 5},
                {0, 3, 0, 0, 7},
                {6, 8, 0, 0, 9},
                {0, 5, 7, 9, 0},
        };

        int n=graph.length;

        ArrayList<Vertex> vertices=new ArrayList<>();
        for(int i=0;i<n;i++) {
            vertices.add(new Vertex(-1, false, Integer.MAX_VALUE));
        }
        vertices.get(0).key=0;


        for (int i=0;i<n;i++){

            int min=find(vertices);
            vertices.get(min).set=true;

            for(int j=1;j<n;j++){
                if(graph[min][j]<vertices.get(j).key&&vertices.get(j).set==false && graph[min][j]!=0){
                    vertices.get(j).key=graph[min][j];
                    vertices.get(j).parent=min;
                }
            }
        }

        System.out.println("Edge    Weight");
        for(int i=1;i<vertices.size();i++){
            System.out.println(vertices.get(i).parent+" - "+i+"  : "+graph[i][vertices.get(i).parent]);
            //System.out.println(vertices.get(i).toString());        }
    }

    static int find(ArrayList<Vertex> vertices){
        int min=Integer.MAX_VALUE,i=0;

        for(int x=0;x<vertices.size();x++){
            if(vertices.get(x).key<min && vertices.get(x).set!=true){
                min=vertices.get(x).key;
                i=x;
            }
        }

        return i;
    }

}

Output:

Knapsack Java

Knapsack Using Greedy Algorithm

Code:
package com.nearur;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
public class KNAPSACK {
 static int capacity=40;

 public static void main(String[] args) {
package com.nearur;

public class Item {

String name;
int value,weight;
public Item(String name, int value, int weight) {
super();
this.name = name;
this.value = value;
this.weight = weight;
}

int compareWeight(Item x) {
if(x.weight>weight) {
return -1;
}return 1;
}

int compareValue(Item x) {
if(x.value>value) {
return 1;
}return -1;
}

int compareratio(Item x) {
if(x.value/x.weight>value/weight) {
return 1;
}return -1;
}

}

  Item [] item=new Item[4];
  item[0]=new Item("I1",100,20);
  item[1]=new Item("I2",90,10);
  item[2]=new Item("I3",40,15);
  item[3]=new Item("I4",50,5);

  ArrayList<Item> knapsack=new ArrayList<>();
  ArrayList<Item> allitems=new ArrayList<>();

  for(int i=0;i<item.length;i++) {
   allitems.add(item[i]);
  }

  Comparator<Item> com=new Comparator<Item>() {
 
   @Override
   public int compare(Item o1, Item o2) {
    return o1.compareratio(o2);
    //return o1.compareValue(o2);
    //return o1.compareWeight(o2);
   }
  };

  Collections.sort(allitems,com);

  for(Item ite:allitems) {
   System.out.println(ite.name);
   if(ite.weight<=capacity) {
    knapsack.add(ite);
    capacity=capacity-ite.weight;
   }
  }

  int mvalue=0,mweight=0;

  for(Item i: knapsack) {
   mvalue +=i.value;
   mweight +=i.weight;
  }

  System.out.println("Total Value: "+mvalue+"\nTotal Weight: "+mweight);
 }
}


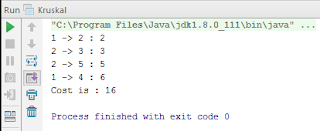
Output: